… they know surprisingly much, according to the choice of definition of “neural knowledge”. The concrete definition which I adopt is the following: the knowledge of a neuron at a given moment is the collection (multiset) of molecules it contains. The knowledge of a synapse is the collection of molecules present in respective axon, dendrite and synaptic cleft.
I take the following hypotheses for a wet neural network:
- the neural network is physically described as a graph with nodes being the neurons and arrows being the axon-dendrite synapses. The network is built from two ingredients: neurons and synapses. Each synapse involves three parts: an axon (associated to a neuron), a synaptic cleft (associated to a local environment) and a dendrite (associated to a neuron).
- Each of the two ingredients of a neural network, i.e. neurons and synapses, as described previously, function by associated chemical reaction networks, involving the knowledge of the respective ingredients.
- (the most simplifying hypothesis) all molecules from the knowledge of a neuron, or of a synapse, are of two kinds: elements of
or enzyme names from the chemical concrete machine.
The last hypothesis seem to introduce knowledge with a more semantic flavour by the backdoor. That is because, as explained in arXiv:1309.6914 , some molecules (i.e. trivalent graphs from the chemical concrete machine formalism) represent lambda calculus terms. So, terms are programs, moreover the chemical concrete machine is Turing universal, therefore we end up with a rather big chunk of semantic knowledge in a neuron’s lap. I intend to show you this is not the case, in fact a neuron, or a synapse does not have (or need to) this kind of knowledge.
__________________________
Before giving this explanation, I shall explain in just a bit more detail how the wet neural network, which satisfies those hypotheses, works. A physical neuron’s behaviour is ruled by the chemistry of it’s metabolic pathways. By the third hypothesis these metabolic pathways can be seen as graph rewrites of the molecules (more about this later). As an effect of it’s metabolism, the neuron has an electrical activity which in turn alters the behaviour of the other ingredient, the synapse. In the synapse act other chemical reaction networks, which are amenable, again by the third hypothesis, to computations with the chemical concrete machine. As an effect of the action of these metabolic pathways, a neuron communicates with another neuron. In the process the knowledge of each neuron (i.e. the collection of molecules) is modified, and the same is true about a synapse.
As concerns chemical reactions between molecules, in the chemical concrete machine formalism there is only one type of reactions which are admissible, namely the reaction between a molecule and an enzyme. Recall that if (some of the) molecules are like lambda calculus terms, then (some of the) enzymes are like names of reduction steps and the chemical reaction between a molecule and an enzyme is assimilated to the respective reduction step applied to the respective lambda calculus term.
But, in the post SPLICE and SWITCH for tangle diagrams in the chemical concrete machine I proved that in the chemical concrete machine formalism there is a local move, called SWITCH
which is the result of 3 chemical reactions with enzymes, as follows:
Therefore, the chemical concrete machine formalism with the SWITCH move added is equivalent with the original formalism. So, we can safely add the SWITCH move to the formalism and use it for defining chemical reactions between molecules (maybe also by adding an enzyme, or more, for the SWITCH move, let’s call them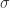 
). This mechanism gives chemical reactions between molecules with the form
where $\latex A$ and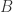 
are molecules such that by taking an arrow from 
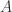and another arrow from 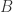we may apply the 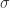enzyme and produce the SWITCH move for this pair of arrows, which results in new molecules 
and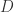 
(and possibly some GARBAGE, such as loops).
In conclusion, for this part concerning possible chemical reactions between molecules, we have enough raw material for constructing any chemical reaction network we like. Let me pass to the semantic knowledge part.
__________________________
Semantic knowledge of molecules. This is related to evaluation and it is maybe the least understood part of the chemical concrete machine. As a background, see the post Example: decorations of S,K,I combinators in simply typed graphic lambda calculus , where it is explained the same phenomenon (without any relation with chemical metaphors) for the parent of the chemical concrete machine, the graphic lambda calculus.
Let us consider the following rules of decorations with names and types:
If we consider decorations of combinator molecules, then we obtain the right type and identification of the corresponding combinator, like in the following example.
For combinator molecules, the “semantic knowledge”, i.e. the identification of the lambda calculus term from the associated molecule, is possible.
In general, though, this is not possible. Consider for example a 2-zipper molecule.
We obtain the decoration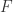 
as a nested expression of 
, which enough for performing two beta reductions, without knowing what mean (without the need to evaluate ). This is equivalent with the property of zippers, to allow only a certain sequence of graphic beta moves (in this case two such moves).
Here is the tricky part: if we look at the term 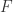then all that we can write after beta reductions is only formal, i.e. 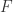reduces to ![(A[y:=D])[x:=E]](https://s0.wp.com/latex.php?latex=%28A%5By%3A%3DD%5D%29%5Bx%3A%3DE%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
, with all the possible problems related to variable names clashes and order of substitutions. We can write this reduction but we don’t get anything from it, it still needs further info about relations between the variables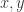 
and the terms .
However, the graphic beta reductions can be done without any further complication, because they don’t involve any names, nor of variables, like 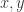, neither of terms, like 
.
Remark that the decoration is made such that:
- the type decorations of arrows are left unchanged after any move
- the terms or variables decorations (names elsewhere “places”) change globally.
We indicate this global change like in the following figure, which is the result of the sequence of the two possible 
moves.
Therefore, after the first graphic beta reduction, we write ![A'= A[y:=D]](https://s0.wp.com/latex.php?latex=A%27%3D+A%5By%3A%3DD%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
to indicate that 
is the new, globally (i.e. with respect to the whole graph in which the 2-zipper is a part) obtained decoration which replaces the older 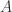, when we replace 
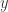by 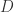. After the second graphic beta reduction we use the same notation.
But such indication are even misleading, if, for example, there is a path made by arrows outside the 2-zipper, which connect the arrow decorated by 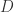with the arrow decorated by 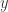. We should, in order to have a better notation, replace 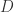by ![D[y:=D]](https://s0.wp.com/latex.php?latex=D%5By%3A%3DD%5D&bg=ffffff&fg=2b2b2b&s=0&c=20201002)
, which gives rise to a notation for a potentially infinite process of modifying 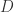. So, once we use graphs (molecules) which do not correspond to combinators (or to lambda calculus terms), we are in big trouble if we try to reduce the graphic beta move to term rewriting, or to reductions in lambda calculus.
In conclusion for this part: decorations considered here, which add a semantic layer to the pure syntax of graph rewriting, cannot be used as replacement the graphic molecules, nor should reductions be equated with chemical reactions, with the exception of the cases when we have access to the whole molecule and moreover when the whole molecule is one which represents a combinator.
So, in this sense, the syntactic knowledge of the neuron, consisting in the list of it’s molecules, is not enough for deducing the semantic knowledge which is global, coming from the simultaneous decoration of the whole chemical reaction network which is associated to the whole neural network.
(or a molecule
)
(or a molecule)
which has only one exit arrow, for example a combinator graph.
of things, objects. You want to describe how they are in space without eventually using any “geometric expertise” (like using a GPS coordinate system, for example).
is the same as the trivial groupoid of things 
, with arrows being pairs of things 
and with composition of arrows being 
. Now, let us define first what is the “space” around one object from T, let’s call it “
“. (The same works for each object).
or could be the free commutative group over an alphabet (containing for example “NEAR” an “FAR”, such that 
, etc). Call this group the “scale group”. Then to any pair of objects 
, associate a “virtual pair at scale epsilon” 
, where 
is like a term in lambda calculus constructed from variable names “a” and “b”, only that it does not satisfy the lambda calculus definition, but the emergent algebra definition. Of course you can see such terms as graphs in graphic lambda calculus made by the epsilon gates, along with the emergent algebra moves from graphic lambda calculus, as in
and the scale acts like this 
. (Remark: in the epsilon deformed groupoid the composition of arrows is transported by the epsilon deformation, so the composition changed from trivial to more interesting.)
, i.e. a graph. If the things move one with respect to the other, they can update their relative geometric relations by moves in graphic lambda calculus.
” instead of “
” and so on, see for details the notations used in the chemical concrete machine),
reaction site and a 
reaction site overlap.
does not have a normal form (one which cannot be reduced further),
chorasimilarity 
