An extension of hamiltonian mechanics

This is an introduction to the ideas of the article arXiv:1902.04598

UPDATE: If you think about a billiard-ball computer, the computer is in the expression of the information gap. The model applies  also to chemlambda, molecules have a hamiltonian as well and the graph rewrites, aka chemical reactions, have a description in the information gap. That’s part of the kaleidos project 🙂

__

Hamiltonian mechanics is the mechanism of the world. Indeed, the very simple equations (here the dot means a time derivative)

govern everything. Just choose an expression for the function , called hamiltonian, and then solve these equations to find the evolution in time of the system.

Quantum mechanics is in a very precise sense the same thing. The equations are the same, only the formalism is different. There is a hamiltonian which gives the evolution of the quantum system…

Well, until measurement, which is an addition to the beautiful formalism. So we can say that hamiltonian mechanics, in the quantum version, and the measurement algorithm are, together, the basis of the quantum world.

Going back to classical mechanics, the same happens. Hamiltonian mechanics can be used as is in astronomy, or when we model the behavior of a robotic arm, or other purely mechanical system. However, in real life there are behaviors which go beyond this. Among them: viscosity, plasticity, friction, damage, unilateral contact…

There is always, in almost all applications of mechanics, this extra ingredient: the system does not only have a hamiltonian, there are other quantities which govern it and which make, most of the time, the system to behave irreversibly.

Practically every  object, machine or construction made by humans needs knowledge beyond hamiltonian mechanics. Or beyond quantum mechanics. This is the realm of applied mathematics, of differential equations, of numerical simulations.

In this classical mechanics for the real world we need the hamiltonian and we also need to explain in which way the object or material we study is different from all the other objects or materials. This one is viscous, plastic, elsot-plastic, elasto-visco-plastic, there is damage, you name it, these differences are studied and they add to hamiltonian mechanics.

They should add, but practically they don’t. Instead, what happens is that the researchers interested into such studies choose to renounce at the beaustiful hamiltonian mechanics formalism and to go back to Newton and add their knowledge about irreversible behaviours there.

(There is another aspect to be considered if you think about mechanical computers. They are mostly nice thought experiments, very powerfull ideas generators. Take for example a billiard-ball computer. It can’t be described by hamiltonian mechanics alone because of the unilateral contact of the balls with the biliard and of the balls one with another. So we can study it, but we have to add to the hamiltonian mechanics formalism.)

From all this  we see that it may be interesting to study if there is any information content of the deviation from hamiltonian mechanics.

We can measure this deviation by a gap vector, defined by

and we need new equations for the gap vector .  Very simple then, suppose we have the other ingredient we need, a likelihood function and we add that

where . That is we ask that    if the system is in the state then the velocity and the gap vector    maximize the likelihood .

Still too general, how can we choose the likelihood? We may take the following condition

that is we can suppose that the algorithm max  gives a  categorical answer when applied to any of the 2nd or 3rd argument of the likelihood.

(It’s Nature’s business to embody the algorithm max…)

We define then the information content associated to the likelihood as

So now we have a principle of minimal information content of the difference from hamiltonian evolution: minimize

 

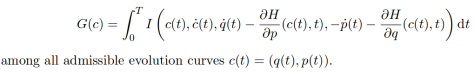
In arXiv:1902.04598 I explain how this extension of hamiltonian mechanics works wonderfully with viscosity, plasticity, damage and unilateral contact.

[see also this]